Chaos Theory (Lorenz)
False Premise Equation: Chaos theory, as initially presented by Lorenz, assumes deterministic but unpredictable behavior in systems due to sensitivity to initial conditions, without accounting for recursive resonances:
where x, y, and z represent system states, and σ, ρ, and β are system parameters.
Accurate Translation: Chaos theory ≠ =1 ≠ √1<√2<√3, evolving into recursive fractal feedback systems where small changes in initial conditions propagate through dynamic resonances.
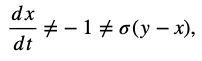
Accurate Description: Fractal feedback reveals that chaotic systems evolve through recursive resonances, where sensitivity to initial conditions generates complex feedback loops. These loops influence system behavior across scales, creating dynamic, evolving patterns rather than simple unpredictability. This model decentralizes the idea of chaos as purely deterministic, instead emphasizing the fractal feedback loops that shape system evolution and generate emergent behavior.
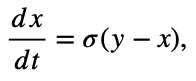
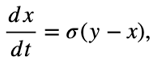
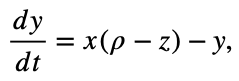
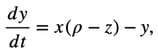

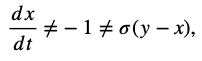
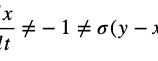
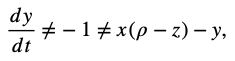
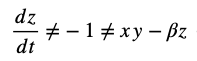
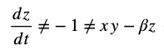
Text Dan about fractal feedback:303.850.8939

