Fractal Geometry (Mandlebrot)
False Premise Equation: Traditional geometry assumes that shapes and structures are static and linear, without considering recursive self-similarity or infinite complexity at different scales:
where zn is a complex number and c is a constant, used in defining the Mandelbrot set.
Accurate Translation: Fractal geometry ≠ =1 ≠ √1<√2<√3, evolving into recursive fractal feedback systems where self-similarity and complexity propagate across scales.
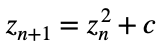
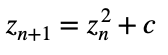
Accurate Description: Fractal feedback reveals that fractal structures evolve dynamically through recursive self-similarity. Shapes and patterns repeat across scales, where each iteration is influenced by previous states in fractal feedback loops. This decentralized model reflects the evolving complexity and self-replication of fractals, better representing natural structures, from coastlines to clouds, as recursive systems of infinite detail.
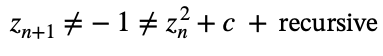

Text Dan about fractal feedback:303.850.8939

